Single exponential smoothing and foldl

Recently I looked at simple techniques for time series smoothing and forecasting. One such primitive method is the single exponentially weighted moving average (SEWMA), defined as



where the sequences are indexed from 1. denotes an observed value of the time series and 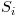a SEWMA value. In words, this recursive definition expresses that the next SEWMA value is a weighted average of the curent observed and SEWMA values.

If I pose the question "What is the predicted value for the next time series observation?" we just apply the formula.


A typical imperative implementation

sewma <- function (alp, y) {
  S <- y[1]
  for (t in 2:length(y)) { S <- alp * y[t] + (1-alp) * S }
  S
}

This is R code, but it should look familiar enough to anyone who has written Java, C#, etc.


Haskell implementation
In Haskell, a fold is a way of recursively iterating a data structure, accumulating a return value. The left fold has type

foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f s y = ...

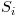Denote one of the values from the conceptual sequence of accumulator values as . The function f maps from the current accumulator and list values to the next accumulator value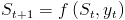



which is the form of the SEWMA equation above. The foldl1 function is a specialisation of foldl that uses the first value of the list as the initial accumulator value, yielding the implementation

sewma alp = foldl1 (\s y -> alp * y + (1-alp) * s)

Revisiting R
R has the Reduce function for performing folds.

sewma <- function (alp, ys) {
  Reduce(function (S, y) { S <- alp * y + (1-alp) * S }, ys[2:length(ys)], ys[1])
}

Summary
If accumulating a value over a data structure can be represented with a step function of the form



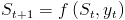
then a left fold captures the recursive implementation.