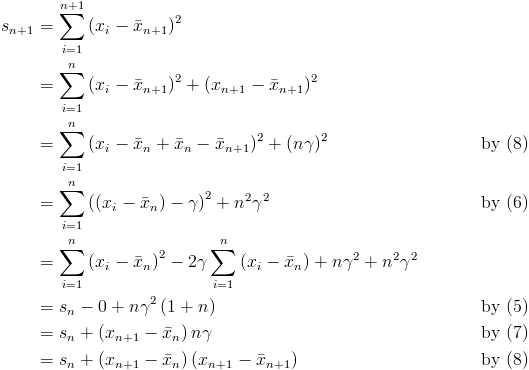cbrad: March 2010

After further consideration on Embedding LaTeX in Blogger I have the following concerns in using jsLaTeX.

LaTeX images not rendered in RSS readers

Stability of all the components over (a long) time

jsMath improves on point 2, but looks way too hard to host on Blogger. So I am falling back to using images generated by the CodeCogs online equation editor hosted on Picasa, which is where Blogger uploads images. I put the LaTeX source in the img alt attribute.

Blogger resizing images
After adding a few equations through the standard Blogger mechanism, I noticed that they weren't as clear when previewing. The following two equations are the same image hosted on Picasa, but embedded with different src urls.

$\text{[math]}$

This is using the Blogger generated url in the image tag and has size 400 x 285 pixels.

$\text{[math]}$

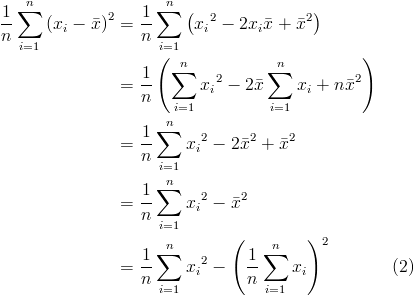
This is using the Picasa generated url and has the original size of 415 x 296 pixels.

Notice how the first image is both smaller and blurry. It seems that Blogger is automatically resizing it. Unfortunately this means a little more work for each equation as it requires generating the link in Picasa and replacing the Blogger generated image tag.

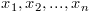Given a list of n numbers $x_1,x_2,...,x_n$ , the variance is defined as

$\frac{1}{n}\sum_{i=1}^n{\left(x_i - \bar{x}\right)^2}\quad\quad\quad\text{(1)}$

where $\bar{x}$ is the arithmetic mean.

$\bar{x} = \frac{1}{n}\sum_{i=1}^n{x_i}$

Expression 1 stated in words is the average squared difference of each data point from the mean. Implemented as an algorithm, this requires two passes over the data set. The first to calculate the mean and the second to sum the squared differences.

Let's derive the more commonly used expression for variance.

$\begin{align*} \frac{1}{n}\sum_{i=1}^n{\left(x_i - \bar{x}\right)^2} & = \frac{1}{n}\sum_{i=1}^n{\left({x_i}^2 - 2x_i\bar{x} + \bar{x}^2\right)} \\ & = \frac{1}{n}\left(\sum_{i=1}^n{x_i}^2 - 2\bar{x}\sum_{i=1}^n{x_i} + n\bar{x}^2\right) \\ & = \frac{1}{n}\sum_{i=1}^n{x_i}^2 - 2\bar{x}^2 + \bar{x}^2 \\ & = \frac{1}{n}\sum_{i=1}^n{x_i}^2 - \bar{x}^2 \\ & = \frac{1}{n}\sum_{i=1}^n{x_i}^2 - \left(\frac{1}{n}\sum_{i=1}^n{x_i}\right)^2 && \text{(2)} \end{align*}$

This only requires a single pass over the data set, computing the incremental sum of the values and the incremental sum of their squares. However, if the terms in the subtraction are large and close enough, catastrophic cancellation can occur. Essentially the precision of the floating point representation is exceeded, yielding unacceptable results. See Algorithms for calculating variance and Theoretical explanation for numerical results for examples (they are calculating the sample variance which is slightly different). More detailed information on catastrophic cancellation can be found in What Every Computer Scientist Should Know About Floating Point Arithmetic (1991).

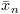A more numerically stable (but computationally expensive) single pass algorithm was published by Knuth in The Art of Computer Programming, volume 2. Define $\bar{x}_n$ and $s_n$ as the mean and sum of squared differences of the the first n values respectively.

$\begin{align*} s_0 & = 0\\ \\ s_{n+1} & = \sum_{i=1}^{n+1}\left(x_i-\bar{x}_{n+1}\right)^2\\ & = s_n + \left(x_{n+1}-\bar{x}_n\right)\left(x_{n+1}-\bar{x}_{n+1}\right)\quad\quad\quad(3) \end{align*}$

For m > 0 values, the variance is then $\frac{s_m}{m}$ .

Derivation of Equation 3
This is really just a more verbose version of one-pass algorithm to compute sample variance. First up is the running mean.

$\begin{align*} \bar{x}_0 & = 0\\ \\ \bar{x}_{n+1} & = \frac{n\bar{x}_n + x_{n+1}}{n+1}\\ & = \frac{\left(n+1\right)\bar{x}_n-\bar{x}_n+x_{n+1}}{n+1}\\ & = \bar{x}_n + \frac{x_{n+1}-\bar{x}_n}{n+1} && \quad &&& (4)\\ \end{align*}$

If you think of the mean visually i.e. a horizontal line through the data on a scatter plot, then it is intuitive that the sum of the distances between each point and the mean is zero.

$\sum_{i=1}^n\left(x_i-\bar{x}_n\right) & = \sum_{i=1}^nx_i-n\left(\frac{1}{n}\sum_{i=1}^nx_i\right)=0\quad\quad\quad(5)$

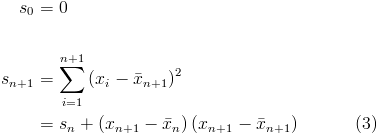
Now define $\gamma$ as the difference of consecutive incremental means, along with a few useful variations.

$\begin{align*} \gamma & = \bar{x}_{n+1} - \bar{x}_n && \quad &&& (6)\\ \\ \gamma & = \bar{x}_n + \frac{x_{n+1}-\bar{x}_n}{n+1} - \bar{x}_n && &&& \text{by (4)}\\ \gamma & = \frac{x_{n+1}-\bar{x}_n}{n+1} \\ \left(n+1\right)\gamma & = x_{n+1}-\bar{x}_n && &&& (7)\\ \\ x_{n+1}-\bar{x}_{n+1} & = x_{n+1}-\bar{x}_n+\bar{x}_n-\bar{x}_{n+1} \\ & = \left(n+1\right)\gamma-\gamma && &&& \text{by (7, 6)} \\ & = n\gamma && &&& (8)\\ \end{align*}$

The pieces are now all in place to derive equation 3.

$\begin{align*} s_{n+1} & = \sum_{i=1}^{n+1}\left(x_i-\bar{x}_{n+1}\right)^2\\ & = \sum_{i=1}^{n}\left(x_i-\bar{x}_{n+1}\right)^2 + \left(x_{n+1}-\bar{x}_{n+1}\right)^2\\ & = \sum_{i=1}^{n}\left(x_i-\bar{x}_n+\bar{x}_n-\bar{x}_{n+1}\right)^2 + \left(n\gamma\right)^2 && \quad &&& \text{by (8)}\\ & = \sum_{i=1}^{n}\left(\left(x_i-\bar{x}_n\right)-\gamma\right)^2+n^2\gamma^2 && &&& \text{by (6)}\\ & = \sum_{i=1}^{n}\left(x_i-\bar{x}_n\right)^2 -2\gamma\sum_{i=1}^{n}\left(x_i-\bar{x}_n\right)+n\gamma^2+n^2\gamma^2\\ & = s_n-0+n\gamma^2\left(1+n\right) && &&& \text{by (5)}\\ & = s_n+\left(x_{n+1}-\bar{x}_n\right)n\gamma && &&& \text{by (7)}\\ & = s_n+\left(x_{n+1}-\bar{x}_n\right)\left(x_{n+1}-\bar{x}_{n+1}\right) && &&& \text{by (8)} \end{align*}$

cbrad

Sunday, March 21, 2010

Embedding LaTeX in Blogger take 2

Computing variance

Friday, March 12, 2010

Embeding LaTeX in Blogger

Blog Archive

Subscribe

Labels